\[ \newcommand{\ping}{\text{PING}} \] Open membership P2P systems are plagued by security issues and DHTs are no exception [1]. In this post, I will try to summarize my understanding of one attempt at mitigating some of the security issues found in the Kademlia DHT [2] in adversarial environments. The resulting work [3] is named S/Kademlia1, and it is significant in that it underpins a number of practical DHT implementations, including the libp2p DHT spec..
Types of Attacks
Kademlia provides some protection against certain types of attacks, but is vulnerable to others.
Sybil attacks. Sybil identities are groups of ids an attacker can create to register multiple nodes within the network [1], typically with the intent of disrupting routing or another ill intent. Kademlia does not provide any mechanism to prevent this. Kademlia also does not preclude an attacker from choosing its ids, meaning that not only an attacker can create multiple identities, they can also choose the position in the network they want to create these identities in.
Eclipse attacks. In Eclipse attacks [1] an attacker occupies node ids along multiple routing paths (possibly using Sybil identities) so that it can cut off (or “eclipse”) selected parts of the network. Kademlia provides some natural level of resiliency to eclipse attacks as nodes will not update their \(k\)-buckets with newly discovered nodes unless:
- the \(k\)-bucket in which the node is supposed to go into is not full;
- the \(k\)-bucket is full, but the least recently seen node in it fails to respond to a \(\ping\) message.
Point (2) is what makes the network resilient to attackers attempting to replace routing entries with entries pointing to rogue nodes. Point (1) implies that the network is vulnerable until it reaches critical mass. \(k\)-buckets within the near vicinity of a node can remain underpopulated for a long time, however, meaning that nodes could remain exposed for longer depending on how routing is implemented.
Churn attacks. The fact that Kademlia nodes do not insert new nodes into their routing tables unless old ones stop responding to \(\ping\) messages also precludes what the authors define as “churn attacks”, where an attacker inserts nodes into the network and then creates artificial churn to destabilize it. To see why this is harder with Kademlia, note that even if an attacker manages to insert nodes into someone else’s routing table, these nodes will get dropped as soon as they stop responding. Larger adversaries could probably still disrupt the network by inserting many nodes and then bringing them down all at the same time, but this is harder to do.
Adversarial routing. Adversaries can hijack query paths and respond with adversarial routing information so that lookups fail. Because lookup paths converge in Kademlia – and this was originally considered desirable as it made caching easier – a single rogue node may be able to disrupt all paths that converge on it. Authors propose that routing through disjoint routing paths can mitigate the issue (at the cost of caching), and estimate the probability of lookup failures in an adversarial environment as follows.
They start by assuming that for a certain path length range \([1, k] \subset \mathbb{N}\), we can build \(k\) separate sets of paths containing \(d\) disjoint paths of that length each. They then assume, implicitly, that a lookup can select one of these paths at random to send a message.
We can then compute the probability of a success by attempting to compute the probability that we pick a path without an adversary. Because we are picking a path uniformly at random, this probability will equate with the probability that one such path exists2, which is what we will attempt to compute next.
Paths of different lengths are distributed according to \(h(i)\), which we can take to be a discrete pdf, and we know that the fraction of adversarial nodes in the network is \(m\). Let \(L\) be a random variable denoting the length of a path drawn uniformly at random, and let \(S_i\) be the number of paths of length \(i\) containing no adversarial nodes.
We can now compute the probability that we draw a path that does not contain adversarial nodes:
\[ \begin{align} p_s = \mathbb{P}\left(\bigcup_{i=1}^{k} L = i\cap S_i \geq 1\right) &\stackrel{1}{=}\\ \sum_{i = 1}^{k} \mathbb{P}\left(L = i\cap S_i \geq 1\right) &= \\ \sum_{i = 1}^{k}\mathbb{P}(L = i \mid S_i = 1)\mathbb{P}(S_i \geq 1) &\stackrel{2}{=} \\ \sum_{i = 1}^{k}\mathbb{P}(L=i)\mathbb{P}(S_i \geq 1) &= \\ \sum_{i = 1}^{k} h(i)\mathbb{P}(S_i \geq 1)& \tag{1} \end{align} \] Where \(\stackrel{1}{=}\) follows from the fact that path sets are disjoint (i.e. you cannot select paths of different lenghts at the same time), and \(\stackrel{2}{=}\) follows from the fact that the probability with which we select a path of length \(i\) is independent from whether or not the set of paths of length \(i\) contain adversarial nodes3.
We now focus on \(\mathbb{P}(S_i \geq 1)\), the probability that we have at least one path of length \(i\) with no adversarial nodes which, recall, is the same as the probability of picking a path of length \(i\) with no adversarial nodes when selecting uniformly at random. We will express this as \(1\) minus the probability that all paths have adversarial nodes. Since the fraction of adversarial nodes is \(m\), a path of length \(i\) has no adversarial nodes with probability \((1 - m)^i\)4, and therefore a path has at least one adversarial node with probability \(1 - (1 - m)^i\).
Since we have \(d\) disjoint paths, we can then compute the probability that all paths have at least one adversarial node by taking \((1 - (1 - m)^i)^d\). Finally, the probability that at least one path of length \(i\) has no adversarial nodes is \(1 - (1 - (1 - m)^i)^d\). Plugging that into Eq. (1), we get:
\[ p_s = \sum_{i = 1}^{k} h(i)\mathbb{P}(S_i \geq 1) = \sum_{i = 1}^{k} h(i)\left(1 - (1 - (1 - m)^i)^d\right) \]
Although I have done my best to try to interpret what authors were trying to calculate (they only show the equation for \(p_s\)) this does nevertheless look weird, particularly having \(h(i)\) to weight the selection when we assume there are \(d\) disjoint paths for a given length: these two things appear to contradict each other. If the formula should be expressing the probability of success for a random selection of size \(d\) over all paths, on the other hand, then I am not convinced it is correct.
S/Kademlia
Sybil Identities and Crypto Puzzles
S/Kademlia introduces protection against Sybil attacks by means of two distinct crypto puzzles. These are shown in Fig. 1, which is taken from the paper [3]. The first puzzle – referred to as the “static” puzzle – constrains the node to find a public key whose hash starts with \(c_1\) zeroes. Then a second crypto puzzle – referred to as the “dynamic” puzzle – forces the node to find a number \(x\) such that the hash of \(\text{node_id} \oplus x\) starts with \(c_2\) zeroes, where \(\oplus\) is the XOR of the binary representation of both numbers.
Both puzzles ensure that it is not easy to create node ids; i.e., it is not easy to create Sybil identities, and although it is clear that the static puzzle needs to be run when a new node id is created, it is unclear when and now the second puzzle fits into the bigger picture.
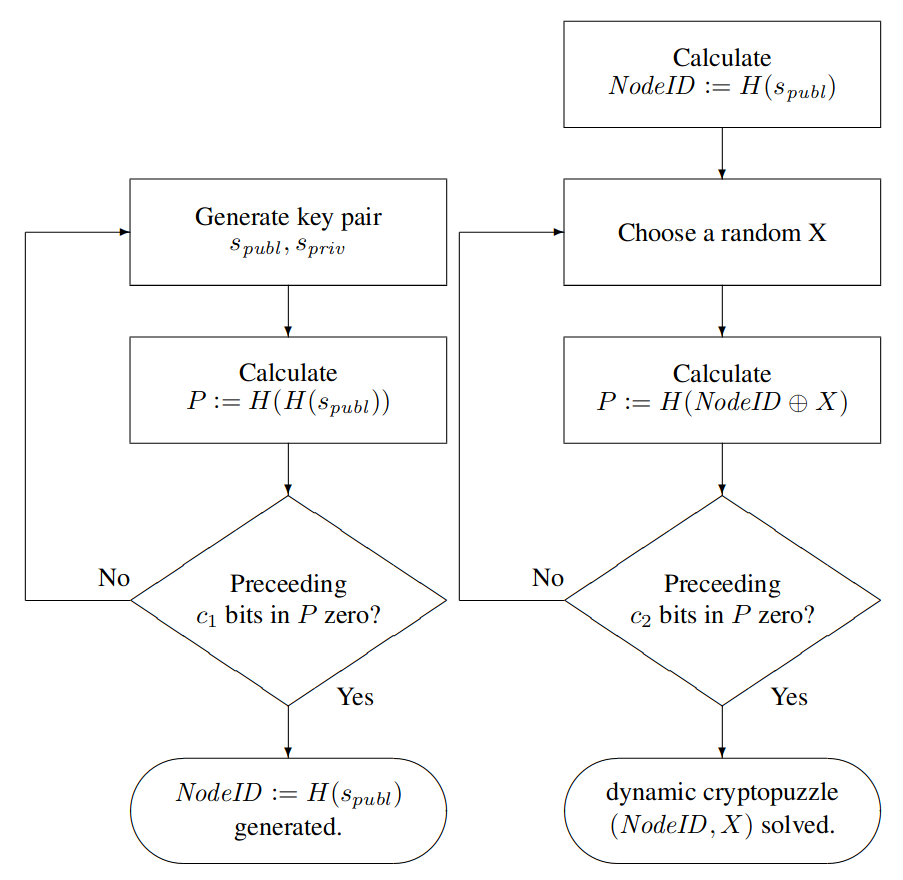
Figure 1: Static (left) and dynamic (right) crypto puzzles
Sibling Lists
S/Kademlia also introduces the notion of sibling lists, which point to nodes that replicate a key-value pair. Unlike Kademlia, S/Kademlia has a separate parameter \(s\) for siblings so that the size of the replication set for a key-value pair is different from the parameter \(k\), which is used for routing redundancy (i.e., in Kademlia, \(s = k\)).
One of the goals here is to simplify the \(k\)-bucket splitting rules. Kademlia uses a dynamic binary tree whose leaves are \(k\)-buckets. A \(k\)-bucket gets split whenever a new contact comes in a full \(k\)-bucket which contains the node’s own id. The problem is with unbalanced DHTs, like the one in Fig. 2 (a).
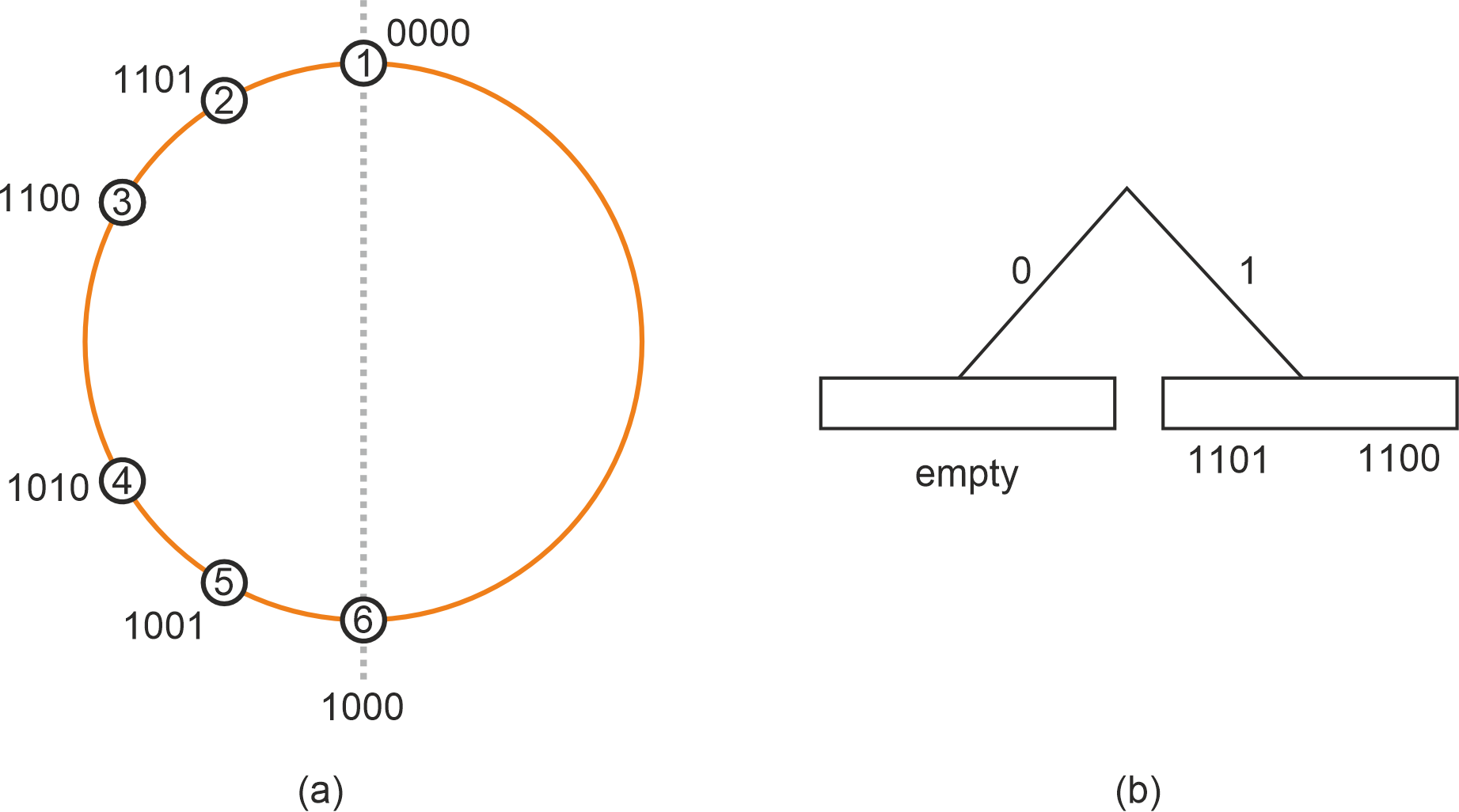
Figure 2: (a) non-uniform DHT and (b) Routing table at \(0000\) after all nodes join.
Suppose for the sake of argument that \(k = 2\). If nodes were to join in the specified order; i.e. \(0000\) joins first, then \(1101\), then \(1100\), and so on, then the first contacts to be seen by node \(0000\) would be \(1101\) and \(1100\), which would fill up the \(k\)-bucket with leading prefix \(1xxx\) (Figure 2 (b)). This would cause nodes \(1010\) and \(1001\) to be discarded on join as the \(k\)-bucket would be already full, leading the closest neighborhood of \(0000\) to be undersampled.
Kademlia therefore relaxes this rule by allowing the bucket to be split if the incoming nodes are closer to the receiving node than any node in its \(k\)-buckets. This means that when \(1010\) joins, node \(0000\) would figure that \(1010\) is closer to itself than any other node it knows, and therefore would allow the \(k\)-bucket to be split (Fig. 3 (a)).
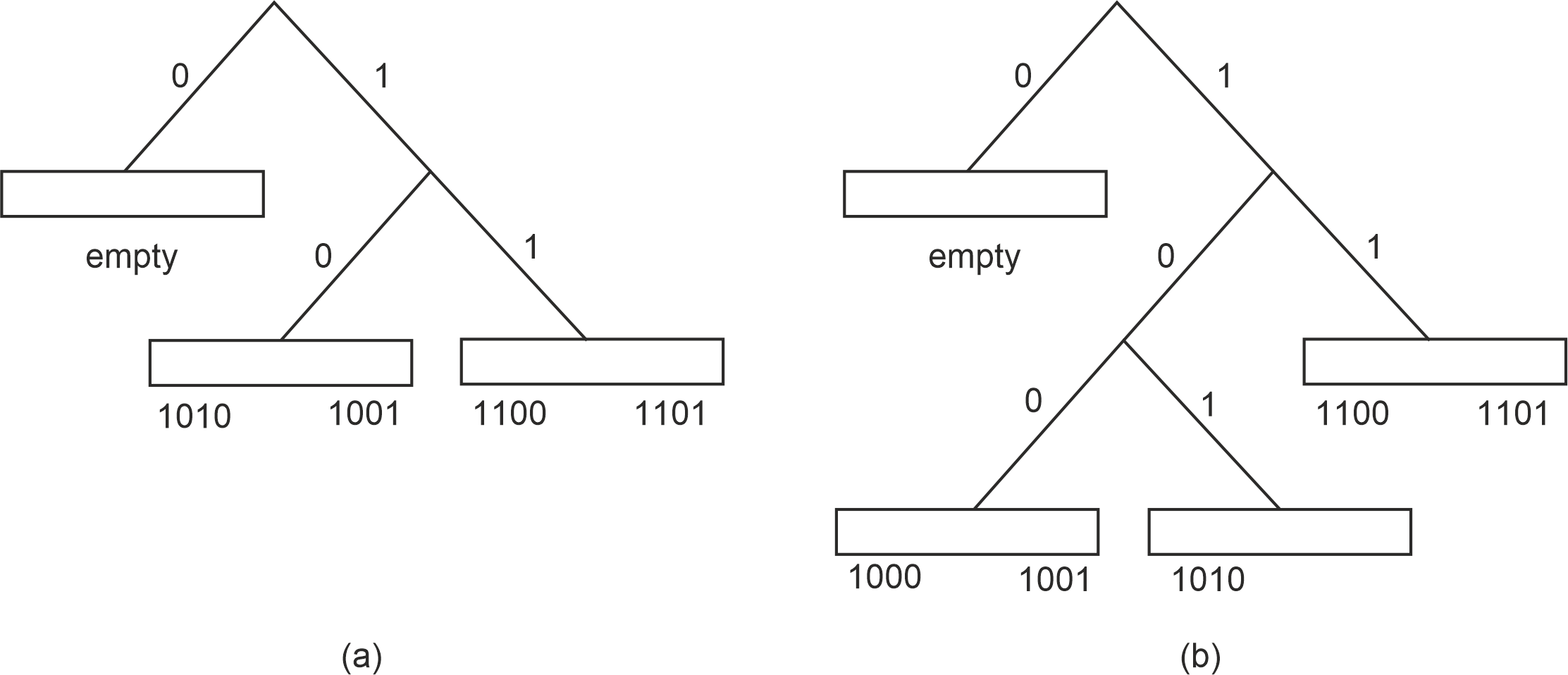
Figure 3: Table with relaxed splitting after (a) \(1010\) and \(1001\) join and (b) \(1000\) join.
Authors argue that this is complex and unnecessary, and that using a sibling list of size \(s\) makes things simpler as it does not require having relaxed bucket splits. They therefore adopt a single splitting rule, and do away with the buckets in the \([0, 2^{i-1})\) interval entirely, keeping the sibling list instead.
<to be continued… :-)>
Which one could assume, rather unsurprisingly, stands for Secure Kademlia.↩︎
Which is a very frequentist thing to say. :-)↩︎
Note that this would not be true had we not broken down the \(S_i\) by path length, as longer paths are more likely to contain adversarial nodes than shorter ones↩︎
Making the usual simplification that \(m\) remains constant as we draw nodes from the set↩︎