Distributed Consensus with Unreliable Channels

Synchronous Systems

To make matters simpler, we will discuss this result in the context of synchronous distributed systems [1]. A synchronous distributed system is a simplified model in which we assume that processes execute in lock-step rounds. At each round, each process:

1. generates outgoing messages to its neighbors;
2. processes incoming messages from its neighbors;
3. based on messages received, performs internal computations and updates its state.

This is easier to reason about than “regular” distributed systems because we do not have to worry about messages taking too long to be delivered, being delivered out of order, or about processes that are slow or lag behind others: by the beginning of the next round, all messages will have been delivered, and all computation will have been completed. There is no bound on the size of messages or the amount of computation done that can be done at each round.

An example of a synchronous execution of two processes is shown in Fig. 1.

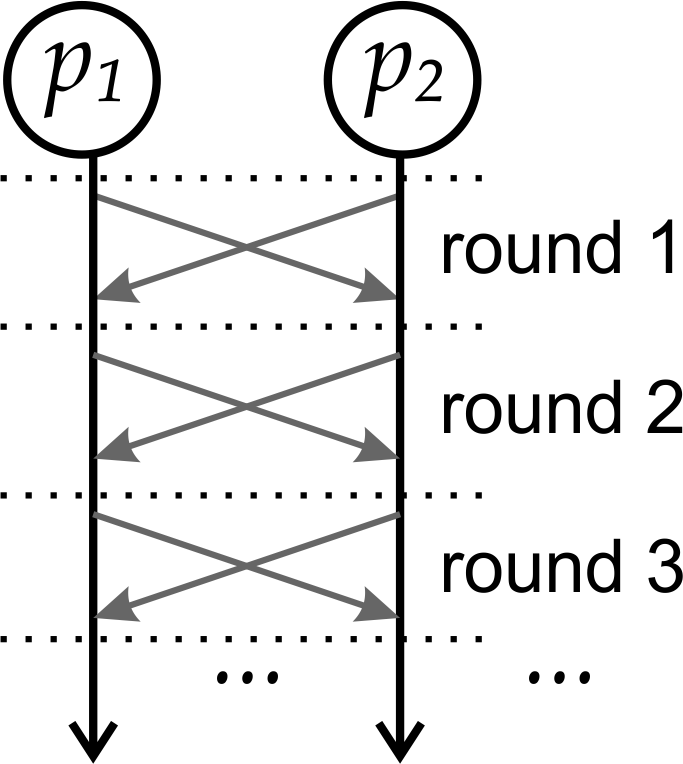
Figure 1: Two processes exchanging messages in a synchronous distributed system.

Consensus in Synchronous Systems

We are now ready to define what “solving” consensus means. Let \(p_1\) and \(p_2\) be two processes connected by a single, unreliable network link (Fig. 2). Each process starts by picking a value \(v\) from \(\{0,1\}\) (which could mean, for instance, “commit” or “abort”¹). Then, at the end of our consensus algorithm, we want both processes to have decided on either \(1\) or \(0\). For consensus to be solved, such decision must respect three properties:

Figure 2: Two processes connected by an unreliable network link.

1. Agreement. No two processes decide on different values.
2. Validity. If all processes start with value \(v\), then all processes must decide on \(v\).
3. Termination. Eventually, all processes decide on some value.

Condition (2) helps us exclude trivial algorithms such as “always decide \(\{0\}\)”. With those definitions in place, we can state our theorem:

Theorem. Let \(p_1\) and \(p_2\) be two processes connected by an unreliable network link. Then there is no algorithm that can solve consensus in this setting.

Proof. The proof will be by contradiction. Suppose there were some algorithm A which did solve consensus in our case. For the sake of argument let us assume, without loss of generality, that \(p_1\) and \(p_2\) have initially chosen \(\{1\}\) as their starting value.

We make the further assumption that processes send a message to each other at every round (recall our distributed system is synchronous). This is without loss of generality as well: you can imagine that processes could simply send empty messages if they wanted to not send anything at a given round.

If \(A\) solves consensus, it means that it eventually terminates, so that there is a round \(r \in \mathbb{N}\) such that, by that round, both processes have to have decided. Again, since both processes started with \(\{1\}\) and \(A\) solves consensus, then by the validity property both must have, by round \(r\), decided \(\{1\}\). This is shown in Fig. 3 as execution \(\alpha\).

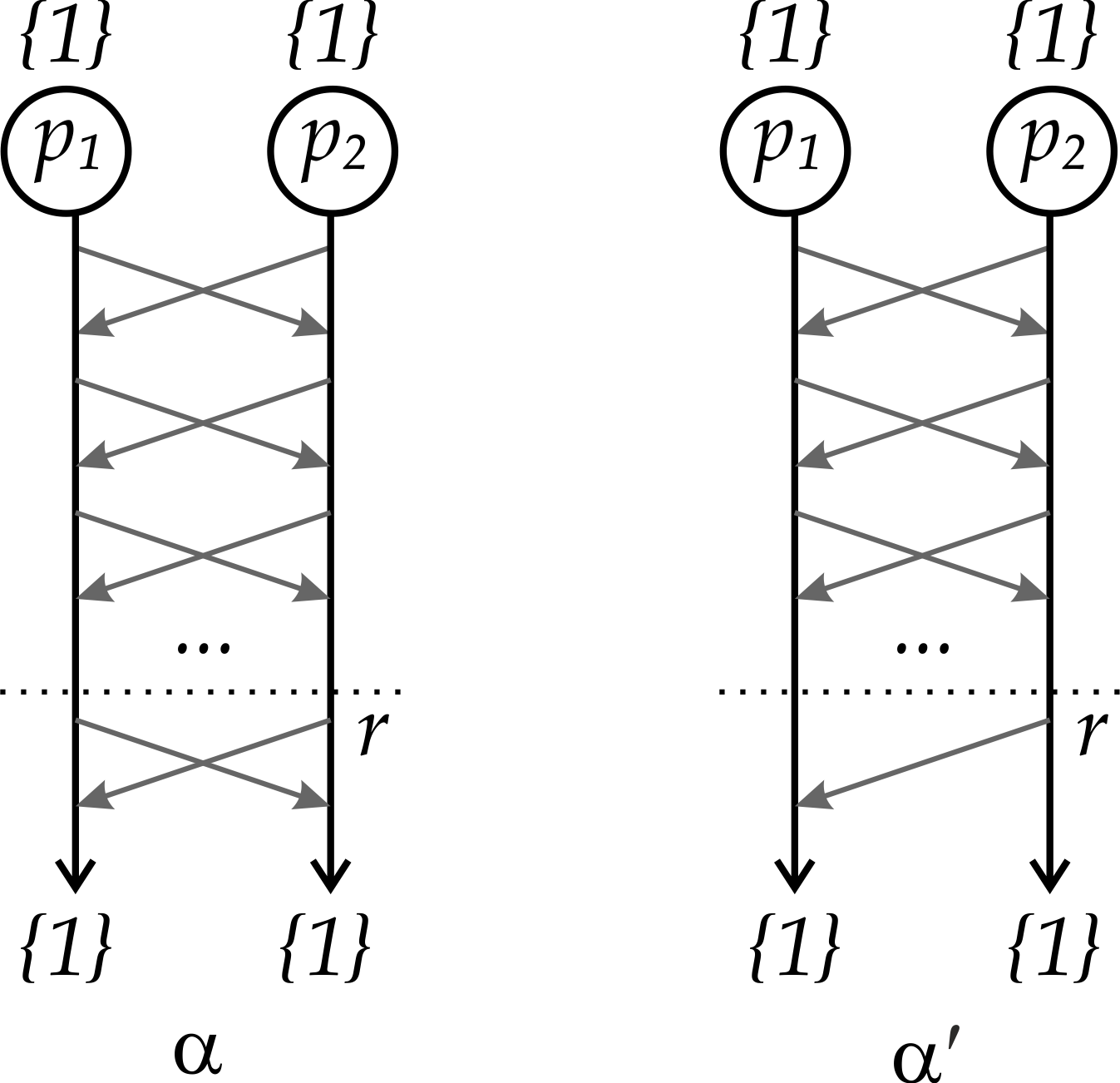
Figure 3: Executions \(\alpha\) and \(\alpha^{\prime}\), with decision by round \(r\).

Now comes the interesting part. If our network channel is unreliable, this means that the last message in \(\alpha\) may have failed to be delivered, leading to alternative execution \(\alpha^{\prime}\), also shown in Fig. 3. Now note that since \(p_1\) receives the exact same set of messages in \(\alpha^{\prime}\) as it did in \(\alpha\), then \(\alpha^{\prime}\) is indistinguishable from \(\alpha\) from the point of view of \(p_1\). This means that if \(p_1\) decides \(\{1\}\) in \(\alpha\), then it must also decide \(\{1\}\) in \(\alpha^{\prime}\).

As for \(p_2\), the execution is different, so it has two options: it either decides \(\{0\}\) because of the missing message, or it decides \(\{1\}\). If it decides \(\{0\}\), then the agreement property is violated and \(A\) does not solve consensus. It must be, therefore, that \(p_2\) also decides \(\{1\}\).

From here, we can apply this procedure recursively until we peel off every single message exchange in \(\alpha\), getting to execution \(\alpha_{11}\) (Fig. 4) where both processes still have to decide \(\{1\}\), even though no messages have been delivered. We can now march towards the contradiction.

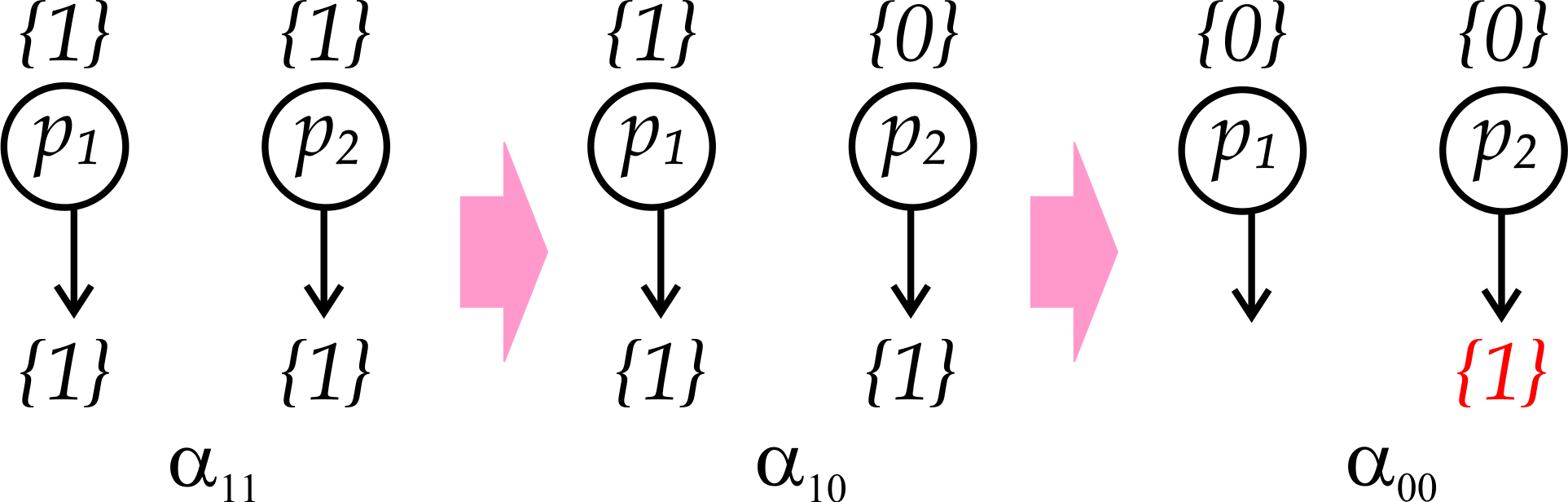
Figure 4: Executions \(\alpha_{11}\), \(\alpha_{10}\), and \(\alpha_{00}\).

By looking at execution \(\alpha_{10}\) (Fig. 4), in which \(p_1\) starts with \(\{1\}\) and \(p_2\) starts with \(\{0\}\), we see that \(\alpha_{10}\) is indistinguishable, from the point of view of \(p_1\), from \(\alpha_{11}\). It must be, therefore, that \(p_1\) decides \(\{1\}\) in \(\alpha_{11}\) and, by the agreement property, it must also be that \(p_2\) decides \(\{1\}\) in \(\alpha_{10}\).

But now look at execution \(\alpha_{00}\), in which both \(p_1\) and \(p_2\) start with \(\{0\}\). Clearly, \(\alpha_{00}\) is indistinguishable from \(\alpha_{10}\) from the point of view of \(p_2\), so it must decide \(\{1\}\). But this violates validity, which states that if all processes start with \(v\) (\(\{0\}\), in this case), then \(v\) is the only possible decision value: a contradiction. \(\blacksquare\)

The key to the impossibility result lies in the requirement that the algorithm terminates despite the loss of arbitrarily many messages. Indeed, if we were willing to give up termination, then the finitely numbered round \(r\) upon which our proof hinges would no longer exist, and the result would fall apart. But giving up termination does not seem like such a great idea either - how is an algorithm that is not guaranteed to terminate of any use?

Again, the key here is that reliability issues tend to be temporary; e.g., you can usually overcome a transiently faulty channel by retrying a transmission enough times. Even more serious issues, such as network partitions, are usually fixed eventually. What happens in practice, then, is that consensus algorithms are designed so that they give up progress guarantees (or rather, liveness guarantees) as long as faults are happening, but resume making progress once faulty behavior subsides, and eventually terminate correctly as long as: i) faults do not keep occurring “incessantly”²; and ii) the faults that do occur do not extend beyond the fault assumptions made by the algorithm. One of the most iconic of these algorithms is Paxos, which I will talk about in a future post.